@DCMT: A Direct Entire-Space Causal Multi-Task Framework for Post-Click Conversion Estimation

主要参考作者在知乎文章：ICDE 2023 论文解读 | DCMT：基于因果纠偏的直接全空间多任务转化率预测模型 - 知乎

DCMT模型（A Direct Entire-Space Causal Multi-Task Framework for Post-Click Conversion Estimation），核心的因果关系图 #card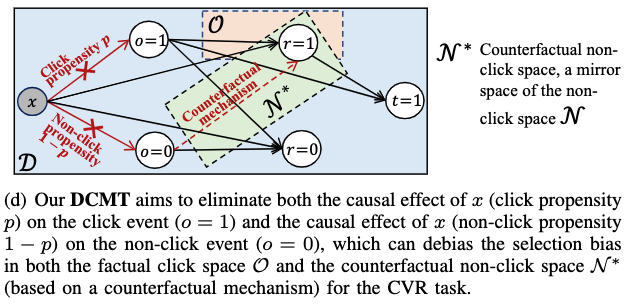

需要直接在全曝光空间去纠偏，而不是只在点击空间（例如IPW）或者间接在全曝光空间（DR）上纠偏。

• 在全曝光空间训练模型的好处就是 #card

  • （1）数据稀疏问题得到缓解

  • （2）训练空间和推断空间直接对齐了

• 在全曝光空间训练CVR模型存在最大的瓶颈问题就是：#card

  • （1）全曝光空间里，对于转化任务而言，存在大量的假负样本。在全曝光空间里，由于不存在“未点击->转化”这样的正样本，这些样本会混在“未点击->未转化”样本中充当假负样本。这些假负样本可能仅仅是因为曝光位置、曝光风格原因，没有被用户察觉到或者点击到。但是如果这些样本被用户点击了，是可以转化的。如果在全曝光空间训练，CVR模型过度拟合这些真假难辨的转化负样本，CVR的预测结果则会偏低。

  • （2）另外，在全曝光样本空间直接训练CVR模型，选择偏差问题仍然存在。所以需要在全曝光空间进行纠偏而不单单在点击空间进行纠偏（如IPW和DR）。这是因为，如果我们认同IPW的思想，即在点击样本空间，点击倾向性会对点击空间样本造成选择偏差。那么在未点击空间，同样也会有不点击倾向性导致选择偏差。

由于受到用户在做转化决策的过程的启发，我们提出了事实样本空间（factual space）和反事实样本空间（counterfactual space）的概念。这里的事实空间和反事实空间如下图所示

• 从概率角度去分析，如果一个用户 $u_i$ 购买（转化）一个物品／服务 $v_j$ 的概率是 $p_{i, j}$ ，那么不转化的概率就是 $1-p_{i, j}$ 。假设用户最终决定购买，即转化标签 $r_{i, j}=1$ ，那么我们能得到一个事实的正样本 $<r_{i, j}=1, o_{i, j}=1, x_{i, j}>$ 。然而这个时候，#card

  • $<r_{i, j}=0, o_{i, j}=1, x_{i, j}>$ 这个负样本则就不会在事实空间里被观察到了。上面已经分析过了，这个负样本实际上本应该是有 $1-p_{i, j}$ 的概率出现的。

  • 在我们的反事实机制里，这样的负样本，$<r_{i, j}=0, o_{i, j}=1, x_{i, j}>$ ，则会存在于反事实空间中。

  • 我们DCMT模型除了利用事实空间的点击空间 $\mathcal{O}$ 样本来预测事实的CVR，还会利用反事实的点击空间 $\mathcal{N}^*$ 样本（事实的未点击样本状态取反而得）来预测反事实CVR。

  • 同时通过以上的分析，我们发现，事实的CVR预测值和反事实的 CVR预测值之和应该与 1 的误差要最小。

[[DCMT 模型]]

[[DCMT CVR Loss]]

[[DCMT 无偏估计证明]]

由于逆倾向加权，如果点击率预测值很小或很大，我们的DCMT对应factual loss或counterfactual loss的权重变得很大很大。因此我们也和传统的IPW方法一样采用了Self-Normalization策略。对应的逆倾向权重改成了#card

• factual loss部分：$\frac{\frac{1}{\bar{c}_{i, j}}}{\sum_{(i, j) \in \mathcal{O}} \frac{1}{\hat{o}_{i, j}}}$

• counterfactual loss部分：$\frac{\frac{1}{1-\hat{\sigma}_{i, j}}}{\sum_{(i, j) \in \mathcal{N}^*} \frac{1}{1-\hat{o}_{i, j}}}$

[[在线实验CVR分布对比]]

[[主要超参对DCMT的影响]]

[[用DR实现CVR建模]]

• 优点 #card

  • 这样做的好处是 $\hat{o}_{i, j}$ 和 $\hat{e}_{i, j}$ 只要有一个预测准确，那么DR就能确保CVR无偏估计。另一个隐性的优点是，MTL－DR一定程度上实现全空间的无偏估计，这是因为imputation任务可以在全曝光空间训练。MTL－DR作者的理解是，imputation任务可以利用全曝光空间预测来的cvr loss来帮助CVR任务进行全曝光空间纠偏。

  • 具体无偏证明如下：

  • $$$$

& \text { Bias }^{\text {MTL-DR }}=\left|E_{\mathcal{O}}\left(\mathcal{E}^{\text {MTL-DR }}\right)-\mathcal{E}^{\text {ground-truth }}\right| \
& =\left|\frac{1}{|\mathcal{D}|} \sum_{(i, j) \in \mathcal{D}}\left(\hat{e}{i, j}+\frac{o{i, j} \delta_{i, j}}{\hat{o}{i, j}}\right)-\frac{1}{|\mathcal{D}|} \sum{(i, j) \in \mathcal{D}} e_{i, j}\right| \
& =\frac{1}{|\mathcal{D}|}\left|\sum_{(i, j) \in \mathcal{D}} \frac{\hat{e}{i, j} \hat{o}{i, j}+o_{i, j} \delta_{i, j}-\hat{o}{i, j} e{i, j}}{\hat{o}{i, j}}\right| \
& =\frac{1}{|\mathcal{D}|}\left|\sum{(i, j) \in \mathcal{D}} \frac{\left(o_{i, j}-\hat{o}{i, j}\right) \delta{i, j}}{\hat{o}_{i, j}}\right|=0 .
\end{aligned}

+ 前提条件是：$o_{i, j}-\hat{o}_{i, j}=0$ 或者 $\delta_{i, j}=e_{i, j}-\hat{e}_{i, j}=0$ ，即 $\hat{o}_{i, j}$ 和 $\hat{e}_{i, j}$ 只要有一个预测准确。 + 缺点 #card + 然而上述这种利用imputation任务间接地在全曝光空间纠偏的策略，没有理论以及实验证明它的有效性。实际上，在DCMT工作的实验部分，我们通过实验验证了MTL-DR模型的CVR预测分布，发现没有全曝光样本空间纠偏的效果（具体见下文实验结果部分）。这里可能的原因是：虽然IPW、DR在点击空间纠偏了，把点击率偏高的样本cvr loss的权重调低了，但是能进入点击空间的的点击率普遍偏高，整体调低了也比较难纠偏到随机点击后分布。只有给点击率偏低的未点击空间样本一个较大的权重，这样才有调整整体分布并趋向于随机点击后分布的可能。另外，MTL-DR的无偏的前提条件，在现实环境中，这两个预测值没有一个能确保预测准，因此DR模型的CVR估计的无偏性很难说比IPW好多少。 [[用IPS实现CVR建模]] + 核心思想：IPW的纠偏策略就是给传统CVR loss进行加权纠偏，对应的权重就是 $1 / p(o=1 \mid x), p(o=1 \mid x)$ 就是用户的点击倾向性（点击率预测值）。因此，基于倾向性的因果纠偏模型也需要利用多任务学习框架来分别预测点击率，点击后转化率。#card + 并通过点击率预测值来给转化任务的loss加一个权重来实现纠偏。这里整个纠偏过程就是为了得到上述的 $p(r=1 \mid d o(o=1), x)$ 。 + 因此IPW模型对应的cvr loss function如下： $\mathcal{E}^{\mathrm{IPW}}=\frac{1}{|\mathcal{D}|} \sum_{(i, j) \in \mathcal{D}} \frac{o_{i, j} e\left(r_{i, j}, \hat{r}_{i, j}\right)}{\hat{p}_{i, j}}$ ，其中 $\mathcal{D}$ 是全曝光样本空间，$o_{i, j}$ 就是点击标签，$e\left(r_{i, j}, \hat{r}_{i, j}\right)$ 就是模型转化率预测误差，$\hat{p}_{i, j}$ 就是点击倾向性。 + 在多任务框架下，cvr loss function则变成 $\mathcal{E}^{\mathrm{MTL}-\mathrm{IPW}}=\frac{1}{|\mathcal{D}|} \sum_{(i, j) \in \mathcal{D}} \frac{o_{i, j} e\left(r_{i, j}, \hat{r}_{i, j}\right)}{\hat{o}_{i, j}}=\frac{1}{|\mathcal{D}|} \sum_{(i, j) \in \mathcal{O}} \frac{e\left(r_{i, j}, \hat{r}_{i, j}\right)}{\hat{o}_{i, j}}$ ，其中 $\mathcal{O}$ 表示点击样本空间，上面的点击倾向性 $\hat{p}_{i, j}$ 也被替代成点击任务的预测值 $\hat{o}_{i, j}$ 。 + 优点：点击空间纠偏，实现条件无偏估计 #card + 我们先给出IPW条件无偏的证明过程。 + 首先，先假设我们能够得到所有的转化标签，即能够观察到所有样本的转化情况，因此我们就能得到转化率预测误差的 ground－truth： +

\mathcal{E}^{\text {ground-truth }}=\mathcal{E}(R, \hat{R})=\frac{1}{|\mathcal{D}|} \sum_{(i, j) \in \mathcal{D}} e\left(r_{i, j}, \hat{r}_{i, j}\right)

$$+ 接下来我们比较MTL－IPW模型的转化率误差与ground－truth之间的差异： +$$

\begin{aligned}
& \text { Bias }^{\text {MTL-IPW }}=\left|E_{\mathcal{O}}\left(\mathcal{E}^{\text {MTL-IPW }}\right)-\mathcal{E}^{\text {ground-truth }}\right| \
& =\left|\frac{1}{|\mathcal{D}|} \sum_{(i, j) \in \mathcal{D}} \frac{o_{i, j}\left(r_{i, j}, \hat{r}{i, j}\right)}{\hat{o}{i, j}}-\frac{1}{|\mathcal{D}|} \sum_{(i, j) \in \mathcal{D}} e\left(r_{i, j}, \hat{r}{i, j}\right)\right| \
& =\frac{1}{|\mathcal{D}|}\left|\sum{(i, j) \in \mathcal{D}}\left(\frac{o_{i, j}}{\hat{o}{i, j}}-1\right) e\left(r{i, j}, \hat{r}_{i, j}\right)\right|=0 .
\end{aligned}

+ 也就是 $\frac{o_{i, j}}{\hat{o}_{i, j}}-1=0$ ，即 $o_{i, j}=\hat{o}_{i, j}$（点击率预测准确），就可以确保IPW纠偏后的CVR loss是与 ground－truch的CVR loss－致的。所以IPW无偏估计的前提条件就是点击率预测准确。 + 缺点：没有在全曝光空间上训练转化率模型。#card + 上面的 $\mathcal{E}^{\text {MTL－IPW }}$ 公式也很明显的说明了，IPW只计算点击样本空间 $\mathcal{O}$ 的 CVR loss。